收集树中金币

There exists an undirected and unrooted tree with n nodes indexed from 0 to n - 1. You are given an integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an array coins of size n where coins[i] can be either 0 or 1, where 1 indicates the presence of a coin in the vertex i.

Initially, you choose to start at any vertex in the tree. Then, you can perform the following operations any number of times: 

• Collect all the coins that are at a distance of at most 2 from the current vertex, or
• Move to any adjacent vertex in the tree.

Find the minimum number of edges you need to go through to collect all the coins and go back to the initial vertex.

Note that if you pass an edge several times, you need to count it into the answer several times.

 

Example 1:

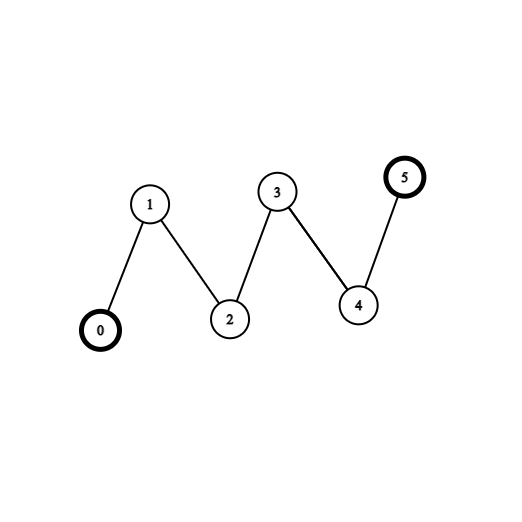
Input: coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]]
Output: 2
Explanation: Start at vertex 2, collect the coin at vertex 0, move to vertex 3, collect the coin at vertex 5 then move back to vertex 2.

Example 2:

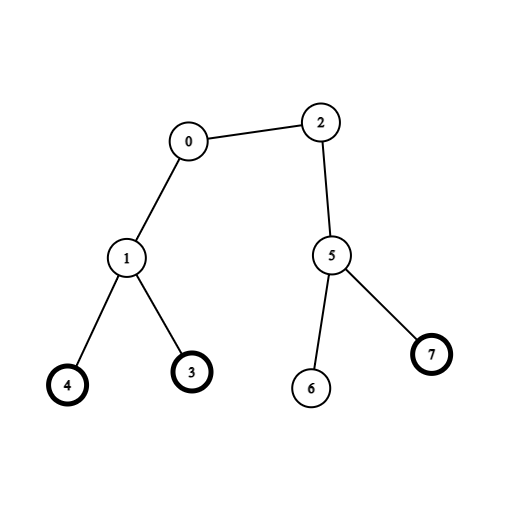
Input: coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]
Output: 2
Explanation: Start at vertex 0, collect the coins at vertices 4 and 3, move to vertex 2,  collect the coin at vertex 7, then move back to vertex 0.

 

Constraints:

• n == coins.length
• 1 <= n <= 3 * 104
• 0 <= coins[i] <= 1
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges represents a valid tree.

// Java Stream solution for the problem
// Problem statement: Given an unrooted tree with n nodes, each node may have a coin. You need to collect all the coins starting from any node and return to the starting node with the minimum number of edges traversed.

import java.util.*;
import java.util.stream.Collectors;

public class SolutionStream {
    private Map<Integer, List<Integer>> graph;
    private int[] coins;
    private int minEdges = 0;

    public int collectTheCoins(int[] coins, int[][] edges) {
        int n = coins.length;
        this.coins = coins;
        graph = Arrays.stream(edges)
                      .flatMap(edge -> Stream.of(Map.entry(edge[0], edge[1]), Map.entry(edge[1], edge[0])))
                      .collect(Collectors.groupingBy(Map.Entry::getKey, Collectors.mapping(Map.Entry::getValue, Collectors.toList())));
        boolean[] visited = new boolean[n];
        dfs(0, visited);
        return minEdges;
    }

    private boolean dfs(int node, boolean[] visited) {
        visited[node] = true;
        boolean hasCoin = coins[node] == 1;
        for (int neighbor : graph.getOrDefault(node, Collections.emptyList())) {
            if (!visited[neighbor]) {
                boolean childHasCoin = dfs(neighbor, visited);
                if (childHasCoin) {
                    minEdges += 2;
                    hasCoin = true;
                }
            }
        }
        return hasCoin;
    }
}

题解的思路是通过拓扑排序来去除树中那些对解决问题没有直接帮助的节点，即那些没有金币且只有一个邻居（叶节点）的节点。首先，构建邻接表和每个节点的邻居数。然后，将所有没有金币的叶子节点加入队列，并通过拓扑排序逐个移除这些节点。经过一轮拓扑排序后，对剩下的树再进行一轮拓扑排序，特别处理有金币的叶子节点。最后，根据剩余的边数计算答案（来回各一次，所以乘以2），返回需要经过的最少边数。

O(n)

O(n)