找到冠军 II

There are n teams numbered from 0 to n - 1 in a tournament; each team is also a node in a DAG.

You are given the integer n and a 0-indexed 2D integer array edges of length m representing the DAG, where edges[i] = [ui, vi] indicates that there is a directed edge from team ui to team vi in the graph.

A directed edge from a to b in the graph means that team a is stronger than team b and team b is weaker than team a.

Team a will be the champion of the tournament if there is no team b that is stronger than team a.

Return the team that will be the champion of the tournament if there is a unique champion, otherwise, return -1.

Notes

• A cycle is a series of nodes a1, a2, ..., an, an+1 such that node a1 is the same node as node an+1, the nodes a1, a2, ..., an are distinct, and there is a directed edge from the node ai to node ai+1 for every i in the range [1, n].
• A DAG is a directed graph that does not have any cycle.

 

Example 1:

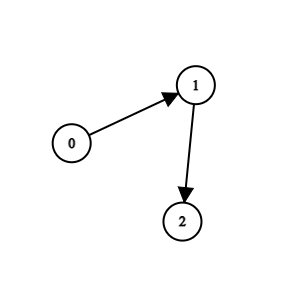
Input: n = 3, edges = [[0,1],[1,2]]
Output: 0
Explanation: Team 1 is weaker than team 0. Team 2 is weaker than team 1. So the champion is team 0.

Example 2:

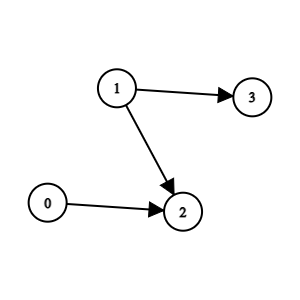
Input: n = 4, edges = [[0,2],[1,3],[1,2]]
Output: -1
Explanation: Team 2 is weaker than team 0 and team 1. Team 3 is weaker than team 1. But team 1 and team 0 are not weaker than any other teams. So the answer is -1.

 

Constraints:

• 1 <= n <= 100
• m == edges.length
• 0 <= m <= n * (n - 1) / 2
• edges[i].length == 2
• 0 <= edge[i][j] <= n - 1
• edges[i][0] != edges[i][1]
• The input is generated such that if team a is stronger than team b, team b is not stronger than team a.
• The input is generated such that if team a is stronger than team b and team b is stronger than team c, then team a is stronger than team c.

/*
题目思路：
使用Java Stream API来实现相同的逻辑，我们可以首先计算每个节点的入度，然后过滤出入度为0的节点。
如果有且只有一个入度为0的节点，那么它就是冠军队伍，否则返回-1。
*/

import java.util.*;
import java.util.stream.*;

public class ChampionTeamStream {
    public int findChampion(int n, int[][] edges) {
        int[] inDegree = new int[n];
        Arrays.stream(edges).forEach(edge -> inDegree[edge[1]]++);
        List<Integer> potentialChampions = IntStream.range(0, n)
                                                    .filter(i -> inDegree[i] == 0)
                                                    .boxed()
                                                    .collect(Collectors.toList());
        return potentialChampions.size() == 1 ? potentialChampions.get(0) : -1;
    }
}

题解通过维护一个包含所有队伍的列表来标记可能的冠军队伍。遍历给定的边，对于每一条边 [u, v]，标记 v 队因为存在比它强的 u 队而不可能是冠军，通过将 champion[v] 设为 -1 实现。最后，所有未被标记为 -1 的队伍即是没有比它强的队伍的候选者。如果存在唯一的候选者，则这个候选者是冠军；如果不存在或存在多个，则返回 -1。

O(n + m)

O(n)