leetcode
leetcode 2651 ~ 2700
网格中的最小路径代价

网格中的最小路径代价

难度:

标签:

题目描述

You are given a 0-indexed m x n integer matrix grid consisting of distinct integers from 0 to m * n - 1. You can move in this matrix from a cell to any other cell in the next row. That is, if you are in cell (x, y) such that x < m - 1, you can move to any of the cells (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1). Note that it is not possible to move from cells in the last row.

Each possible move has a cost given by a 0-indexed 2D array moveCost of size (m * n) x n, where moveCost[i][j] is the cost of moving from a cell with value i to a cell in column j of the next row. The cost of moving from cells in the last row of grid can be ignored.

The cost of a path in grid is the sum of all values of cells visited plus the sum of costs of all the moves made. Return the minimum cost of a path that starts from any cell in the first row and ends at any cell in the last row.

 

Example 1:

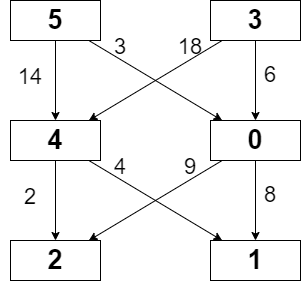
Input: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
Output: 17
Explanation: The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.

Example 2:

Input: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
Output: 6
Explanation: The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 50
  • grid consists of distinct integers from 0 to m * n - 1.
  • moveCost.length == m * n
  • moveCost[i].length == n
  • 1 <= moveCost[i][j] <= 100

代码结果

运行时间: 138 ms, 内存: 21.7 MB

/*
 * Solution Approach using Java Streams: 
 * Similar to the previous solution but using Java Streams for a more functional style.
 */

import java.util.Arrays;
import java.util.stream.IntStream;

public class MinimumPathCostStream {
    public int minPathCost(int[][] grid, int[][] moveCost) {
        int m = grid.length;
        int n = grid[0].length;
        // Initialize dp array with the first row values
        int[] dp = Arrays.copyOf(grid[0], n);
        // Iterate over the rows
        for (int i = 1; i < m; i++) {
            int[] newDp = new int[n];
            Arrays.fill(newDp, Integer.MAX_VALUE);
            // Calculate the minimum cost for each cell in the next row
            for (int j = 0; j < n; j++) {
                final int fromCellValue = grid[i-1][j];
                final int fromCellIndex = j;
                IntStream.range(0, n).forEach(k -> {
                    newDp[k] = Math.min(newDp[k], dp[fromCellIndex] + moveCost[fromCellValue][k] + grid[i][k]);
                });
            }
            dp = newDp;
        }
        // Find the minimum value in the last dp array
        return IntStream.of(dp).min().orElse(Integer.MAX_VALUE);
    }
}

解释

方法:

题解采用了动态规划的方法，从下往上计算每个单元格的最小路径代价。具体思路是，对于每个单元格，计算从当前单元格到下一行所有单元格的代价，加上下一行单元格的已计算的最小路径代价，从而更新当前单元格的最小路径代价。这个过程从倒数第二行开始，一直计算到第一行。最终，第一行的所有单元格都会被更新为从该单元格出发到达最后一行的最小路径代价。返回第一行中代价最小的值作为结果。

时间复杂度:

O(m*n^2)

空间复杂度:

O(1)

代码细节讲解

🦆
为什么在题解中选择从倒数第二行开始向上计算路径代价，而不是从第一行开始向下计算？
▷
从倒数第二行开始向上计算可以直接利用下一行已经计算好的最小路径代价来更新当前行的路径代价，这样可以避免额外的空间开销来存储中间状态。如果从第一行向下计算，则需要额外的数据结构来存储每一行的最小路径代价，因为在计算当前行的最小路径代价时，下一行的最小路径代价还未确定。因此，从下往上的动态规划是空间效率更高的方法。
🦆
在更新每个单元格的最小路径代价时，具体是如何结合下一行的最小路径代价和moveCost数组来计算的？
▷
在更新每个单元格的最小路径代价时，算法首先考察由当前单元格向下一行所有可能的单元格移动的代价。对于每个可能的移动，计算由当前单元格grid[i][j]到下一行某个单元格grid[i+1][k]的移动代价（此代价存储在moveCost[grid[i][j]][k]中），然后将这个移动代价加到下一行该单元格的已知最小路径代价grid[i+1][k]上。所有这些可能的移动路径代价中的最小值就是当前单元格的最新最小路径代价。
🦆
题解中使用了原地更新grid数组的方法来保存状态，这种方法有什么优缺点？
▷
使用原地更新grid数组的方法的优点是节省空间，因为不需要额外的数据结构来存储计算过程中的状态，这使得空间复杂度更低。然而，这种方法的缺点是一旦grid数组被更新，原始的网格信息就会丢失，这意味着如果需要再次使用原始数据或进行其他类型的处理，就必须保留原始数组的副本，这在某些情况下可能会限制算法的灵活性。

相关问题

卖木头块分割回文串 III