关闭分部的可行集合数目
难度:
标签:
题目描述
There is a company with n branches across the country, some of which are connected by roads. Initially, all branches are reachable from each other by traveling some roads.
The company has realized that they are spending an excessive amount of time traveling between their branches. As a result, they have decided to close down some of these branches (possibly none). However, they want to ensure that the remaining branches have a distance of at most maxDistance from each other.
The distance between two branches is the minimum total traveled length needed to reach one branch from another.
You are given integers n, maxDistance, and a 0-indexed 2D array roads, where roads[i] = [ui, vi, wi] represents the undirected road between branches ui and vi with length wi.
Return the number of possible sets of closing branches, so that any branch has a distance of at most maxDistance from any other.
Note that, after closing a branch, the company will no longer have access to any roads connected to it.
Note that, multiple roads are allowed.
Example 1:
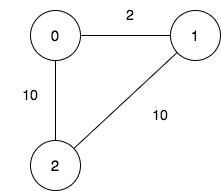
Input: n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]] Output: 5 Explanation: The possible sets of closing branches are: - The set [2], after closing, active branches are [0,1] and they are reachable to each other within distance 2. - The set [0,1], after closing, the active branch is [2]. - The set [1,2], after closing, the active branch is [0]. - The set [0,2], after closing, the active branch is [1]. - The set [0,1,2], after closing, there are no active branches. It can be proven, that there are only 5 possible sets of closing branches.
Example 2:
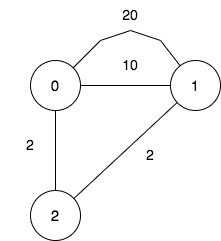
Input: n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]] Output: 7 Explanation: The possible sets of closing branches are: - The set [], after closing, active branches are [0,1,2] and they are reachable to each other within distance 4. - The set [0], after closing, active branches are [1,2] and they are reachable to each other within distance 2. - The set [1], after closing, active branches are [0,2] and they are reachable to each other within distance 2. - The set [0,1], after closing, the active branch is [2]. - The set [1,2], after closing, the active branch is [0]. - The set [0,2], after closing, the active branch is [1]. - The set [0,1,2], after closing, there are no active branches. It can be proven, that there are only 7 possible sets of closing branches.
Example 3:
Input: n = 1, maxDistance = 10, roads = [] Output: 2 Explanation: The possible sets of closing branches are: - The set [], after closing, the active branch is [0]. - The set [0], after closing, there are no active branches. It can be proven, that there are only 2 possible sets of closing branches.
Constraints:
1 <= n <= 101 <= maxDistance <= 1050 <= roads.length <= 1000roads[i].length == 30 <= ui, vi <= n - 1ui != vi1 <= wi <= 1000- All branches are reachable from each other by traveling some roads.
代码结果
运行时间: 172 ms, 内存: 16.8 MB
// 题目思路:
// 1. 使用Floyd-Warshall算法计算每个分部之间的最短距离。
// 2. 使用Stream API遍历所有可能的关闭方案,检查剩余的分部是否都可达且最远距离不超过maxDistance。
// 3. 统计满足条件的方案数量。
import java.util.*;
import java.util.stream.*;
public class Solution {
public int countValidCloseSchemes(int n, int maxDistance, int[][] roads) {
int[][] dist = new int[n][n];
for (int i = 0; i < n; i++) {
Arrays.fill(dist[i], Integer.MAX_VALUE / 2);
dist[i][i] = 0;
}
for (int[] road : roads) {
int u = road[0], v = road[1], w = road[2];
dist[u][v] = Math.min(dist[u][v], w);
dist[v][u] = Math.min(dist[v][u], w);
}
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
return (int) IntStream.range(0, (1 << n)).filter(mask -> {
List<Integer> remaining = IntStream.range(0, n).filter(i -> (mask & (1 << i)) == 0).boxed().collect(Collectors.toList());
if (remaining.isEmpty()) return true;
for (int i = 0; i < remaining.size(); i++) {
for (int j = i + 1; j < remaining.size(); j++) {
if (dist[remaining.get(i)][remaining.get(j)] > maxDistance) {
return false;
}
}
}
return true;
}).count();
}
}
解释
方法:
时间复杂度:
空间复杂度: