可以到达每一个节点的最少边反转次数

There is a simple directed graph with n nodes labeled from 0 to n - 1. The graph would form a tree if its edges were bi-directional.

You are given an integer n and a 2D integer array edges, where edges[i] = [ui, vi] represents a directed edge going from node ui to node vi.

An edge reversal changes the direction of an edge, i.e., a directed edge going from node ui to node vi becomes a directed edge going from node vi to node ui.

For every node i in the range [0, n - 1], your task is to independently calculate the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.

Return an integer array answer, where answer[i] is the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.

 

Example 1:

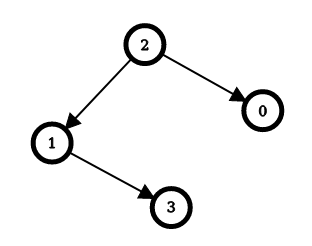
Input: n = 4, edges = [[2,0],[2,1],[1,3]]
Output: [1,1,0,2]
Explanation: The image above shows the graph formed by the edges.
For node 0: after reversing the edge [2,0], it is possible to reach any other node starting from node 0.
So, answer[0] = 1.
For node 1: after reversing the edge [2,1], it is possible to reach any other node starting from node 1.
So, answer[1] = 1.
For node 2: it is already possible to reach any other node starting from node 2.
So, answer[2] = 0.
For node 3: after reversing the edges [1,3] and [2,1], it is possible to reach any other node starting from node 3.
So, answer[3] = 2.

Example 2:

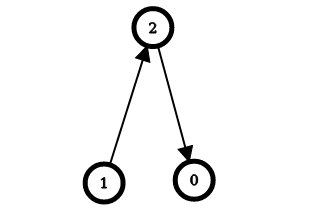
Input: n = 3, edges = [[1,2],[2,0]]
Output: [2,0,1]
Explanation: The image above shows the graph formed by the edges.
For node 0: after reversing the edges [2,0] and [1,2], it is possible to reach any other node starting from node 0.
So, answer[0] = 2.
For node 1: it is already possible to reach any other node starting from node 1.
So, answer[1] = 0.
For node 2: after reversing the edge [1, 2], it is possible to reach any other node starting from node 2.
So, answer[2] = 1.

 

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ui == edges[i][0] < n
• 0 <= vi == edges[i][1] < n
• ui != vi
• The input is generated such that if the edges were bi-directional, the graph would be a tree.

/*
 * 使用Java Stream API来构建图，并计算每个节点的最小反转次数。
 * 利用广度优先搜索（BFS）来计算每个节点作为起点到达其他所有节点的最少反转次数。
 * 用Dijkstra算法求解每个节点作为起点的最短路径。
 */
import java.util.*;
import java.util.stream.*;

public class SolutionStream {
    public int[] minReversals(int n, int[][] edges) {
        List<int[]>[] graph = IntStream.range(0, n).mapToObj(i -> new ArrayList<int[]>()).toArray(ArrayList[]::new);
        Arrays.stream(edges).forEach(edge -> {
            graph[edge[0]].add(new int[]{edge[1], 0});
            graph[edge[1]].add(new int[]{edge[0], 1});
        });

        return IntStream.range(0, n).map(i -> dijkstra(graph, n, i)).toArray();
    }

    private int dijkstra(List<int[]>[] graph, int n, int start) {
        int[] dist = new int[n];
        Arrays.fill(dist, Integer.MAX_VALUE);
        dist[start] = 0;
        PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[1]));
        pq.add(new int[]{start, 0});

        while (!pq.isEmpty()) {
            int[] current = pq.poll();
            int node = current[0];
            int distance = current[1];

            if (distance > dist[node]) continue;

            for (int[] edge : graph[node]) {
                int neighbor = edge[0];
                int weight = edge[1];
                int newDist = dist[node] + weight;
                if (newDist < dist[neighbor]) {
                    dist[neighbor] = newDist;
                    pq.add(new int[]{neighbor, newDist});
                }
            }
        }

        return Arrays.stream(dist).max().orElse(Integer.MAX_VALUE);
    }
}

这个题解采用了深度优先搜索（DFS）来解决问题。首先，构建一个图的邻接表，每个边(u, v)不仅记录目标节点v，还记录这条边的转向，如果是正向（u到v），则标记为1，反之为0。接着，从节点0开始，对图进行一次DFS遍历，计算从节点0出发到达所有节点的最少边反转次数，并记录下来。在这个过程中，计算从任意节点i到每个节点的相对深度以及到达该节点经过的正向边的数量。这些信息用于之后计算从其他节点出发到达所有节点的最少反转次数。最后，使用这些信息，通过一次循环计算出从每个节点出发的最少反转次数。

O(n)

O(n)