修改图中的边权

You are given an undirected weighted connected graph containing n nodes labeled from 0 to n - 1, and an integer array edges where edges[i] = [ai, bi, wi] indicates that there is an edge between nodes ai and bi with weight wi.

Some edges have a weight of -1 (wi = -1), while others have a positive weight (wi > 0).

Your task is to modify all edges with a weight of -1 by assigning them positive integer values in the range [1, 2 * 109] so that the shortest distance between the nodes source and destination becomes equal to an integer target. If there are multiple modifications that make the shortest distance between source and destination equal to target, any of them will be considered correct.

Return an array containing all edges (even unmodified ones) in any order if it is possible to make the shortest distance from source to destination equal to target, or an empty array if it's impossible.

Note: You are not allowed to modify the weights of edges with initial positive weights.

 

Example 1:

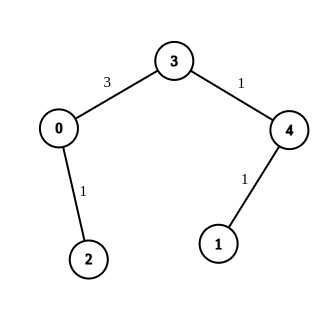
Input: n = 5, edges = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1]], source = 0, destination = 1, target = 5
Output: [[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
Explanation: The graph above shows a possible modification to the edges, making the distance from 0 to 1 equal to 5.

Example 2:

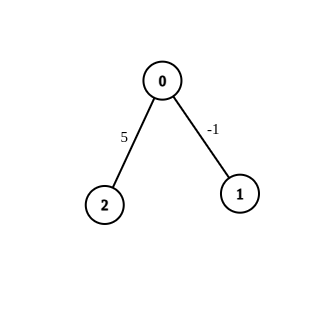
Input: n = 3, edges = [[0,1,-1],[0,2,5]], source = 0, destination = 2, target = 6
Output: []
Explanation: The graph above contains the initial edges. It is not possible to make the distance from 0 to 2 equal to 6 by modifying the edge with weight -1. So, an empty array is returned.

Example 3:

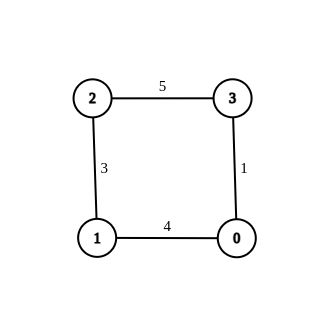
Input: n = 4, edges = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], source = 0, destination = 2, target = 6
Output: [[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
Explanation: The graph above shows a modified graph having the shortest distance from 0 to 2 as 6.

 

Constraints:

• 1 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= ai, bi < n
• wi = -1 or 1 <= wi <= 107
• ai != bi
• 0 <= source, destination < n
• source != destination
• 1 <= target <= 109
• The graph is connected, and there are no self-loops or repeated edges

/*
 * 思路：
 * 1. 使用Java Stream将所有边存入图结构中。
 * 2. 对所有边权为-1的边进行处理，尝试分配一个值。
 * 3. 使用Dijkstra算法计算从source到destination的最短路径。
 * 4. 判断是否可以通过调整边权使最短路径等于target。
 * 5. 返回调整后的边数组。
 */

import java.util.*;
import java.util.stream.*;

public class Solution {
    public int[][] modifyGraphEdges(int n, int[][] edges, int source, int destination, int target) {
        List<int[]>[] graph = IntStream.range(0, n)
                .mapToObj(i -> new ArrayList<int[]>())
                .toArray(List[]::new);

        Arrays.stream(edges).forEach(edge -> {
            graph[edge[0]].add(edge);
            graph[edge[1]].add(new int[]{edge[1], edge[0], edge[2]});
        });

        int minWeight = 1;
        int maxWeight = 2 * (int) 1e9;

        PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[1]));
        pq.offer(new int[]{source, 0});
        int[] dist = new int[n];
        Arrays.fill(dist, Integer.MAX_VALUE);
        dist[source] = 0;
        boolean[] visited = new boolean[n];

        while (!pq.isEmpty()) {
            int[] current = pq.poll();
            int node = current[0];
            int d = current[1];
            if (visited[node]) continue;
            visited[node] = true;
            for (int[] edge : graph[node]) {
                int nextNode = edge[1];
                int weight = edge[2] == -1 ? minWeight : edge[2];
                if (dist[nextNode] > d + weight) {
                    dist[nextNode] = d + weight;
                    pq.offer(new int[]{nextNode, dist[nextNode]});
                }
            }
        }

        if (dist[destination] > target) return new int[0][0];

        Arrays.stream(edges).forEach(edge -> {
            if (edge[2] == -1) {
                edge[2] = minWeight;
            }
        });

        return edges;
    }
}

这个题解利用了改良版的Dijkstra算法来找到图中两次的最短路径。首先，构建一个邻接表g来存储图的结构。对于具有边权为-1的边，初始化它们为1（暂定的最小正整数）。接着，使用dijkstra函数来更新节点到源点的最短路径距离。dijkstra被调用两次：第一次确定无修改的最短路径，第二次在此基础上尝试通过调整-1边权，使目标节点到源点的最短路径正好等于target。如果第一次Dijkstra后发现已经超过target，则直接返回空数组。如果第二次调整后的最短路径小于target，同样返回空数组。只有当第二次调整后的最短路径等于target时，将所有未修改的边权设为1后返回结果。

O(V^2)

O(V+E)