找出最安全路径

You are given a 0-indexed 2D matrix grid of size n x n, where (r, c) represents:

• A cell containing a thief if grid[r][c] = 1
• An empty cell if grid[r][c] = 0

You are initially positioned at cell (0, 0). In one move, you can move to any adjacent cell in the grid, including cells containing thieves.

The safeness factor of a path on the grid is defined as the minimum manhattan distance from any cell in the path to any thief in the grid.

Return the maximum safeness factor of all paths leading to cell (n - 1, n - 1).

An adjacent cell of cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) and (r - 1, c) if it exists.

The Manhattan distance between two cells (a, b) and (x, y) is equal to |a - x| + |b - y|, where |val| denotes the absolute value of val.

 

Example 1:

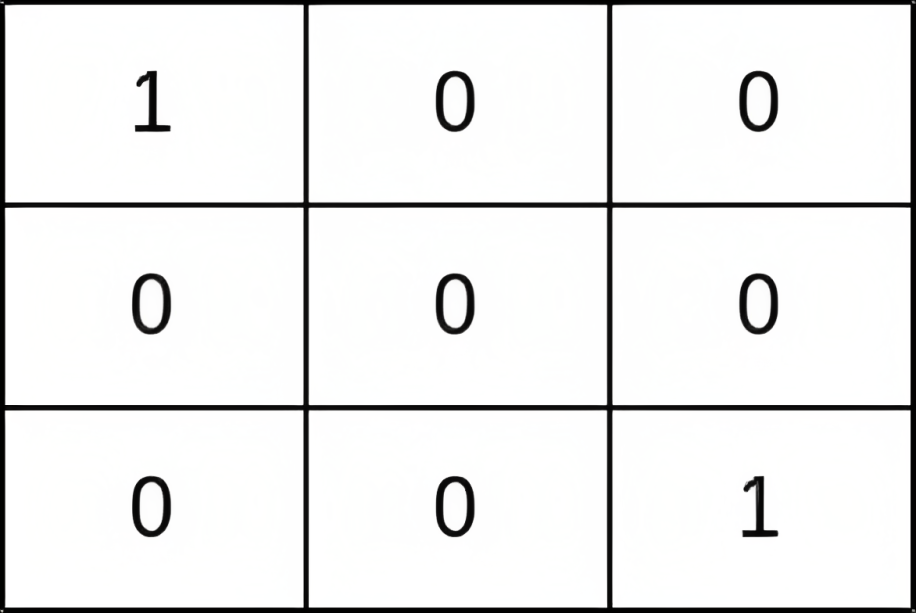
Input: grid = [[1,0,0],[0,0,0],[0,0,1]]
Output: 0
Explanation: All paths from (0, 0) to (n - 1, n - 1) go through the thieves in cells (0, 0) and (n - 1, n - 1).

Example 2:

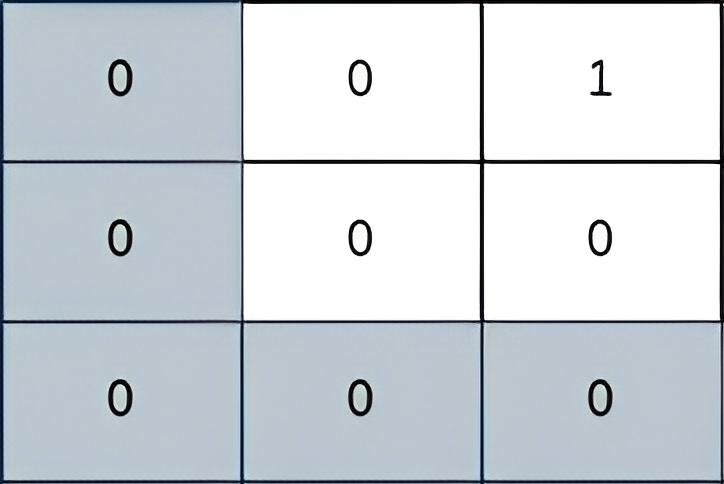
Input: grid = [[0,0,1],[0,0,0],[0,0,0]]
Output: 2
Explanation: The path depicted in the picture above has a safeness factor of 2 since:
- The closest cell of the path to the thief at cell (0, 2) is cell (0, 0). The distance between them is | 0 - 0 | + | 0 - 2 | = 2.
It can be shown that there are no other paths with a higher safeness factor.

Example 3:

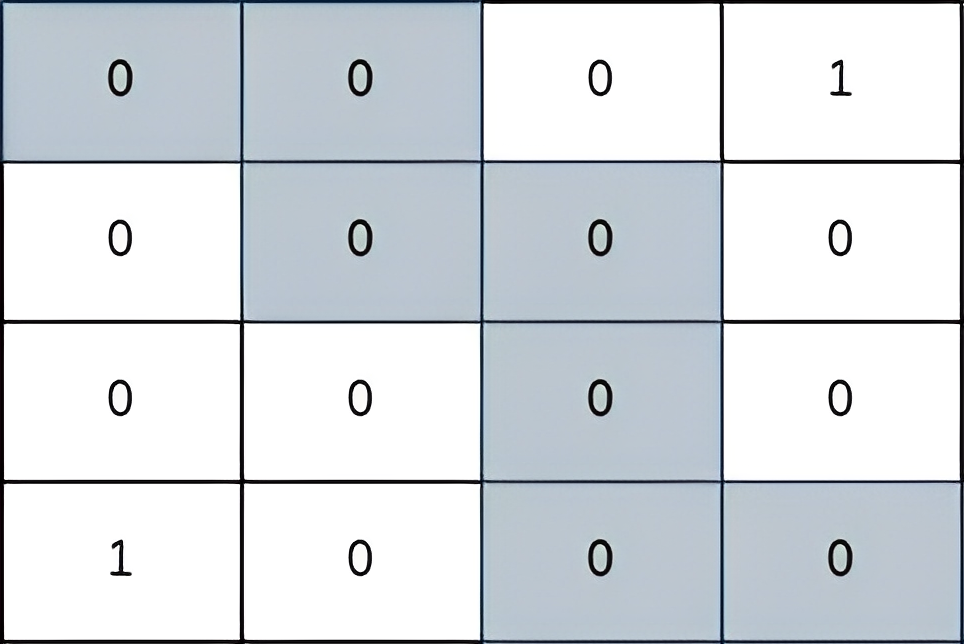
Input: grid = [[0,0,0,1],[0,0,0,0],[0,0,0,0],[1,0,0,0]]
Output: 2
Explanation: The path depicted in the picture above has a safeness factor of 2 since:
- The closest cell of the path to the thief at cell (0, 3) is cell (1, 2). The distance between them is | 0 - 1 | + | 3 - 2 | = 2.
- The closest cell of the path to the thief at cell (3, 0) is cell (3, 2). The distance between them is | 3 - 3 | + | 0 - 2 | = 2.
It can be shown that there are no other paths with a higher safeness factor.

 

Constraints:

• 1 <= grid.length == n <= 400
• grid[i].length == n
• grid[i][j] is either 0 or 1.
• There is at least one thief in the grid.

/* 
 思路： 
 1. 使用Stream API来查找小偷的位置并计算每个单元格的安全系数。 
 2. 使用PriorityQueue来进行BFS搜索，并计算每条路径的最大安全系数。 
*/
import java.util.*;
import java.util.stream.Collectors;
import java.util.stream.IntStream;

public class MaxSafetyPathStream {
    public int maximumSafenessFactor(int[][] grid) {
        int n = grid.length;
        List<int[]> thieves = IntStream.range(0, n)
                .boxed()
                .flatMap(r -> IntStream.range(0, n)
                        .filter(c -> grid[r][c] == 1)
                        .mapToObj(c -> new int[]{r, c}))
                .collect(Collectors.toList());

        int[][] safeness = new int[n][n];
        Arrays.stream(safeness).forEach(row -> Arrays.fill(row, Integer.MAX_VALUE));

        thieves.forEach(thief -> IntStream.range(0, n).forEach(r -> IntStream.range(0, n).forEach(c -> safeness[r][c] = Math.min(safeness[r][c], Math.abs(r - thief[0]) + Math.abs(c - thief[1])))));

        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> b[2] - a[2]);
        pq.offer(new int[]{0, 0, safeness[0][0]});
        boolean[][] visited = new boolean[n][n];
        visited[0][0] = true;
        int[] directions = {-1, 0, 1, 0, -1};

        while (!pq.isEmpty()) {
            int[] current = pq.poll();
            int r = current[0], c = current[1], minSafety = current[2];
            if (r == n - 1 && c == n - 1) {
                return minSafety;
            }

            for (int i = 0; i < 4; i++) {
                int nr = r + directions[i];
                int nc = c + directions[i + 1];
                if (nr >= 0 && nr < n && nc >= 0 && nc < n && !visited[nr][nc]) {
                    visited[nr][nc] = true;
                    pq.offer(new int[]{nr, nc, Math.min(minSafety, safeness[nr][nc])});
                }
            }
        }

        return 0;
    }
}

题解采用了两阶段的广度优先搜索（BFS）策略来求解最大的安全系数。首先，从所有小偷所在的位置开始，对整个网格执行BFS以计算出每个单元格到最近小偷的距离。然后，使用另一轮BFS来找到从起点(0,0)到终点(n-1,n-1)的路径，同时尽可能保持路径上单元格到最近小偷的最小曼哈顿距离最大。这通过追踪当前路径中最小距离的最大值来实现。如果起点或终点有小偷，安全系数直接为0。第一轮BFS结束后，会确定到达每个单元格的最小距离。在第二轮BFS中，会检查从当前单元格到邻近单元格是否能保持或增加这个最小距离的最大值，并优先扩展那些能维持最大距离的路径。

O(n^2 log n)

O(n^2)